Reti Neurali Multilivello
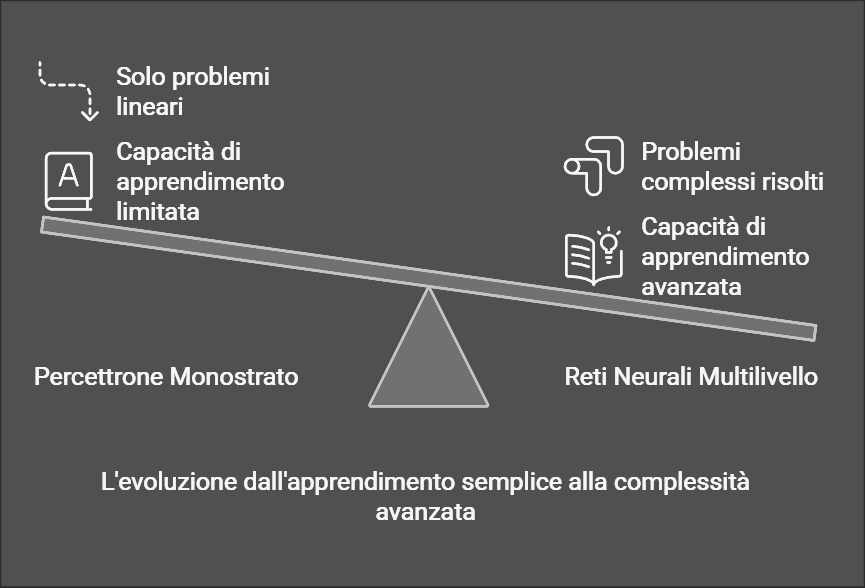
Le reti neurali multilivello (o multistrato) rappresentano un salto concettuale fondamentale rispetto al percettrone di Rosenblatt, superandone i limiti e aprendo la strada all’intelligenza artificiale moderna. Mentre il percettrone monostrato si dimostrò incapace di risolvere problemi non linearmente separabili, l’introduzione di strati nascosti e algoritmi di apprendimento avanzati ha permesso di modellare relazioni complesse nei dati. Questo articolo esplora le origini di questa innovazione, il suo funzionamento, i vantaggi rispetto ai modelli precedenti e gli sviluppi successivi che hanno definito il panorama odierno del deep learning.
Origini e Motivazioni
Il limite del Percettrone e la necessità di un cambiamento
Come evidenziato da Marvin Minsky e Seymour Papert nel 1969, il percettrone monostrato fallisce nel risolvere problemi come la funzione XOR, poiché non può tracciare decisioni non lineari. Questa critica portò a un periodo di scetticismo verso le reti neurali, noto come "inverno dell’IA". Tuttavia, già negli anni ’80, ricercatori come Geoffrey Hinton, David Rumelhart e Yann LeCun ripresero l’idea di reti multilivello, introducendo concetti rivoluzionari come la backpropagation e le funzioni di attivazione non lineari, che permisero di aggirare i limiti del percettrone.
La Nascita del Multi-Layer Perceptron (MLP)
L’MLP, evoluzione diretta del percettrone, aggiunge uno o più strati nascosti tra input e output. Ogni neurone in questi strati applica una trasformazione non lineare (es. sigmoide, tanh, ReLU) ai dati, permettendo alla rete di apprendere rappresentazioni gerarchiche e complesse. Questo approccio risolveva il problema XOR e abilitava la classificazione di pattern arbitrari.
Funzionamento e Architettura
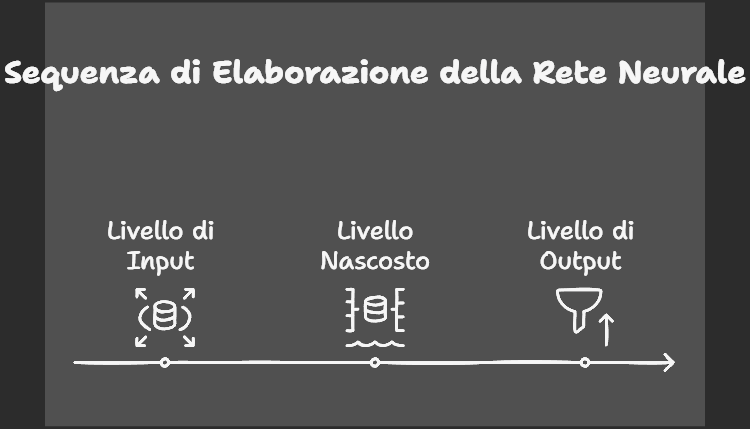
Struttura a Livelli
- Input Layer: Riceve i dati grezzi (es. pixel di un’immagine).
- Hidden Layer(s): Elabora i dati attraverso combinazioni lineari e funzioni di attivazione non lineari.
- Output Layer: Produce il risultato finale (es. classe di un’immagine).
Algoritmo di Apprendimento: Backpropagation
La backpropagation, introdotta negli anni ’80, permette di ottimizzare i pesi della rete calcolando il gradiente dell’errore rispetto a ogni parametro. Il processo si articola in:
- Forward Pass: Calcolo dell’output attraverso i livelli.
- Calcolo dell’Errore: Confronto tra output predetto e reale (es. cross-entropy).
- Backward Pass: Propagazione inversa dell’errore per aggiornare pesi e bias con metodi come la discesa del gradiente.
Funzioni di Attivazione Non Lineari
Le funzioni di attivazione sono funzioni matematiche applicate a ciascun neurone di una rete neurale per decidere se e quanto attivarlo in base all'input ricevuto.
In pratica, trasformano l'input in un output non lineare, permettendo alla rete di apprendere pattern complessi e di modellare funzioni più sofisticate rispetto a una semplice combinazione lineare. Senza una funzione di attivazione, una rete neurale sarebbe solo una combinazione lineare di pesi e input, il che significherebbe che potrebbe risolvere solo problemi linearmente separabili.
Le funzioni di attivazione introducono non linearità, permettendo alla rete di apprendere relazioni più complesse nei dati, come:
- Classificare immagini, testo e audio.
- Prevedere andamenti (forecasting).
- Riconoscere pattern nascosti nei dati.
Come funziona in un neurone artificiale?
Un neurone in una rete neurale segue questi passaggi:
- Riceve gli input: 𝑥1,𝑥2,...,𝑥𝑛.
- Moltiplica gli input per i pesi: 𝑤1,𝑤2,...,𝑤𝑛.
- Somma tutto e aggiunge un bias b: 𝑧 =(𝑤1𝑥1 + 𝑤2𝑥2 + ... + 𝑤𝑛𝑥𝑛) + 𝑏
- Applica la funzione di attivazione 𝑓(𝑧) per produrre l’output finale.
Quindi, la funzione di attivazione decide se e quanto attivare il neurone in base al valore di 𝑧. Le funzioni di attivazione più comuni sono:
Sigmoide (Sigmoid Activation Function)
**Sigmoide**: $$ f(x) = \frac{1}{1+e^{-x}} $$ Utile per output probabilistici.
La funzione sigmoide prende un valore x (che può essere qualsiasi numero reale) e lo trasforma in un numero compreso tra 0 e 1. Se 𝑥 è molto grande, la funzione tende a 1.
- Se 𝑥 è molto piccolo (negativo), la funzione tende a 0.
- Se 𝑥 = 0, la funzione assume il valore 0.5.
Questa proprietà è utile per interpretare il risultato della funzione come una probabilità. Ad esempio, in classificazione binaria (es. email spam o non spam), l'output sigmoide può essere interpretato come la probabilità che un dato appartenga a una certa classe.
| Vantaggi | Svantaggi | Quando usarla |
|---|---|---|
| - Utile per output probabilistici, poiché restringe i valori tra 0 e 1. - Facile da interpretare, specialmente in problemi di classificazione. |
- Problema del "Vanishing Gradient": per valori estremi, il gradiente tende a 0, rallentando l'apprendimento nelle reti neurali profonde. - Non è zero-centrata: i valori di output sono sempre positivi, rallentando la convergenza della rete. |
- Quando serve un output tra 0 e 1 (es. classificazione binaria). - Quando si vuole modellare una probabilità. - Nei livelli di output di una rete neurale per la classificazione binaria. |
ReLU (Rectified Linear Unit)
**ReLU**: $$ f(x) = \max(0, x) $$ Mitiga il vanishing gradient, accelerando l'apprendimento.
- Se x è maggiore di 0, allora 𝑓(𝑥)=𝑥
- Se x è minore o uguale a 0, allora 𝑓(𝑥)=0
Questa funzione elimina i valori negativi e lascia invariati quelli positivi.
| Vantaggi | Svantaggi | Quando usarla |
|---|---|---|
| - Mitiga il problema del Vanishing Gradient, perché per valori positivi la derivata è sempre 1. - Più efficiente rispetto alla Sigmoide perché non utilizza esponenziali (più veloce da calcolare). - Zero-centrata per i valori positivi, accelerando l'apprendimento nelle reti profonde. |
- Problema dei "neuroni morti": se un neurone riceve valori negativi in input per tutto il tempo, la sua uscita sarà sempre zero. - Non è limitata tra 0 e 1, quindi non è adatta per interpretare direttamente probabilità. |
- Strati nascosti delle reti neurali profonde, per velocizzare l'apprendimento. - Quando si vuole evitare il Vanishing Gradient Problem. - Non nei layer di output, perché i valori non sono compresi tra 0 e 1 (meglio usare Sigmoide per output probabilistici o Softmax per classificazione multi-classe). |
Leaky ReLU (Leaky Rectified Linear Unit)
A differenza della ReLU, non annulla completamente i valori negativi, ma li riduce di una frazione αα, permettendo un flusso di gradiente anche per x<0x<0.
- Se x≤0x≤0, f(x)=αx, con α piccolo ma non nullo.
- Se x>0x>0, f(x)=x
Risolve il problema dei neuroni morti di ReLU. f(x)=max(αx,x) (dove α eˋ un iper parametro, tipicamente 0.01)
| Vantaggi | Svantaggi | Quando usarla |
|---|---|---|
| - Mitiga il problema dei "neuroni morti", poiché i gradienti non sono nulli per x<0. - Mantiene l'efficienza computazionale di ReLU. |
- L'iperparametro α deve essere scelto o ottimizzato. - Non garantisce sempre prestazioni migliori rispetto a ReLU (dipende dal contesto). |
- Strati nascosti in reti profonde, soprattutto se si osservano neuroni morti con ReLU. - Alternativa a ReLU in casi di gradienti instabili. |
Softmax
Converte un vettore di logit in probabilità.
La funzione SoftMax normalizza un vettore di valori (x1,x2,...,xNx1,x2,...,xN) in una distribuzione di probabilità, dove ogni elemento è compreso tra 0 e 1 e la somma totale è 1.
| Vantaggi | Svantaggi | Quando usarla |
|---|---|---|
| - Ideale per interpretare output multi-classe come probabilità. - Differenziabile e adatta all'uso con funzioni di perdita come Cross-Entropy. |
- Instabilità numerica per valori molto grandi (risolvibile con tecniche come il "max-shifting"). - Computazionalmente costosa per vettori di grandi dimensioni. |
- Esclusivamente negli strati di output per problemi di classificazione multi-classe (es. riconoscimento di cifre MNIST). |
Tanh (Tangente Iperbolica)
\[ \textbf{Tanh: } f(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} = 2 \cdot \text{Sigmoide}(2x) - 1 \]
E’ simile alla Sigmoide ma è zero-centrata.
Trasforma x in un valore compreso tra -1 e 1. Se x=0, f(x)=0. Per x molto grandi o piccoli, tende a ±1.
| Vantaggi | Svantaggi | Quando usarla |
|---|---|---|
| - Output zero-centrato (-1 a 1), utile per bilanciare i gradienti durante il training. - Adatta a modellare feature con valori negativi (es. segnali audio). |
- Soffre del problema del "Vanishing Gradient" per valori estremi, simile alla Sigmoide. - Meno efficiente di ReLU in reti molto profonde. |
- Strati nascosti in reti non troppo profonde, dove è utile una normalizzazione simmetrica. - Alternativa alla Sigmoide se si preferiscono output negativi e positivi. |
In sintesi
| Funzione | Pro | Contro | Quando usarla? |
|---|---|---|---|
| Sigmoide | Buona per probabilità | Vanishing Gradient | Output di classificazione binaria |
| ReLU | Veloce, evita Vanishing Gradient | Neuroni morti | Layer nascosti di reti profonde |
| Leaky ReLU | Evita neuroni morti | Introduce valori negativi | Layer nascosti quando ReLU fallisce |
| Softmax | Trasforma output in probabilità | Sensibile a outlier | Output di classificazione multi-classe |
| Tanh | Zero-centrata, utile per valori negativi | Vanishing Gradient | Layer nascosti, alternativa alla Sigmoide |
La Classificazione Multi-Classe
La classificazione multi-classe è un tipo di problema di apprendimento supervisionato in cui un modello deve assegnare un'istanza (input) a una delle più di due classi possibili. A differenza della classificazione binaria (che distingue tra due classi, es. "spam" o "non spam"), la classificazione multi-classe può avere più etichette di output, come:
OCR (Riconoscimento Ottico dei Caratteri): Classificare un'immagine come una delle 10 cifre (0-9).
Riconoscimento di oggetti: Identificare se un'immagine contiene un gatto, un cane o un cavallo.
Analisi dei sentimenti: Classificare un testo come "positivo", "neutro" o "negativo".
Differenze principali della RNM rispetto al Percettrone
| Aspetto | Percettrone Monostrato | Reti Multilivello |
|---|---|---|
| Struttura | Singolo strato di output. | Multipli strati nascosti e output. |
| Capacità | Solo problemi linearmente separabili. | Problemi non lineari e complessi. |
| Apprendimento | Regola di Hebb o delta semplice. | Backpropagation + ottimizzatori avanzati (es. Adam). |
| Funzioni di Attivazione | Gradino (0/1). | Non lineari (ReLU, sigmoide, tanh). |
Vantaggi e Applicazioni
Superamento dei Limiti del Percettrone
- Risoluzione di XOR: Grazie agli strati nascosti, l’MLP separa i dati con superfici decisionali non lineari.
- Generalizzazione Migliore: Apprendimento di feature gerarchiche (es.: bordi → forme → oggetti in un’immagine).
Esempi Pratici
- Riconoscimento di Caratteri (OCR): Reti con hidden layer identificano pattern complessi in immagini rumorose.
- Diagnostica Medica: Classificazione di tumori basata su dati radiografici non linearmente correlati.
Sviluppi Successivi e Sfide
Nonostante i progressi significativi, le MLP presentano diverse limitazioni che ne influenzano l'applicabilità pratica. Una discussione critica di queste debolezze è essenziale per comprendere il contesto in cui le MLP sono utilizzate e le sfide che devono affrontare.
1. Sensibilità alla Scelta dei Parametri
Le prestazioni delle MLP dipendono fortemente dalla scelta dei parametri, tra cui:
- Learning Rate: Un valore troppo alto può causare oscillazioni durante l'addestramento, mentre uno troppo basso rallenta la convergenza.
- Numero di Neuroni Nascosti: Troppi neuroni possono portare all'overfitting, mentre pochi possono limitare la capacità della rete di apprendere pattern complessi.
- Funzioni di Attivazione: La scelta della funzione di attivazione influisce sulla velocità di apprendimento e sulla stabilità del modello. Ad esempio, la sigmoide soffre del problema del vanishing gradient, mentre la ReLU può causare neuroni morti.
2. Necessità di Grandi Quantità di Dati
Le MLP richiedono grandi dataset per generalizzare efficacemente. Senza dati sufficienti, il modello rischia di sovra adattarsi ai dati di training (Overfitting), perdendo la capacità di generalizzare su dati non visti. Questo è particolarmente critico in campi come la medicina o la finanza, dove i dati sono spesso limitati o costosi da acquisire.
3. Complessità Computazionale
L'aggiunta di strati nascosti aumenta la complessità computazionale, rendendo l'addestramento delle MLP dispendioso in termini di tempo e risorse. Questo limite è stato parzialmente mitigato da hardware specializzato (GPU, TPU) e ottimizzatori avanzati (es. Adam), ma rimane una barriera per applicazioni in tempo reale o su dispositivi con risorse limitate.
4. Difficoltà nell'Interpretazione
Le MLP sono modelli "black box", il che significa che è difficile interpretare il processo decisionale interno. Questo è un problema critico in settori come la sanità o la giustizia, dove la trasparenza e l'interpretazione delle decisioni sono fondamentali.
5. Vulnerabilità agli Outlier
Le MLP sono sensibili a outlier e rumore nei dati, che possono influenzare negativamente l'apprendimento. Tecniche di preprocessing e regolarizzazione (es. Dropout, Batch Normalization) sono essenziali per mitigare questo problema.
Conclusione
Le reti neurali multilivello (MLP) hanno gettato le basi per lo sviluppo di architetture più sofisticate che oggi dominano il panorama del deep learning. Tra queste, le Convolutional Neural Networks (CNN) e le Recurrent Neural Networks (RNN) rappresentano due innovazioni fondamentali che hanno rivoluzionato rispettivamente l'elaborazione di dati visivi e sequenziali.
Convolutional Neural Networks (CNN)
Le CNN sono state progettate specificamente per l'elaborazione di immagini e video. A differenza delle MLP, che trattano i pixel come input indipendenti, le CNN sfruttano la struttura spaziale dei dati attraverso filtri convoluzionali. Questi filtri permettono di catturare caratteristiche locali, come bordi, texture e forme, in modo gerarchico. Ad esempio:
- Layer Convoluzionali : Estraggono feature di basso livello (bordi, angoli) nei primi strati e feature di alto livello (oggetti, scene) nei layer successivi.
- Pooling Layers : Riducono la dimensionalità dei dati, preservando le informazioni più rilevanti e migliorando l'invarianza a traslazioni e distorsioni.
- Fully Connected Layers : Combinano le feature estratte per produrre una classificazione finale.
Le CNN hanno avuto un impatto enorme su applicazioni reali come:
- Riconoscimento di immagini : Identificazione di oggetti, volti e scene in contesti come la guida autonoma e la sicurezza.
- Diagnostica medica : Analisi di immagini radiografiche per la rilevazione di malattie come tumori o fratture.
- Generazione di contenuti : Creazione di immagini realistiche tramite modelli generativi come GAN (Generative Adversarial Networks).
Recurrent Neural Networks (RNN)
Le RNN sono state progettate per gestire dati sequenziali, come testo, audio e serie temporali. A differenza delle MLP, che assumono input indipendenti, le RNN mantengono uno "stato interno" che consente loro di catturare dipendenze temporali. Varianti avanzate come le Long Short-Term Memory (LSTM) e le Gated Recurrent Units (GRU) hanno risolto problemi come il vanishing gradient, consentendo l'apprendimento di relazioni a lungo termine.
Le RNN trovano applicazione in:
- Traduzione automatica : Modelli come Transformer hanno sostituito le RNN tradizionali, ma le basi teoriche rimangono cruciali.
- Riconoscimento vocale : Conversione della voce in testo per assistenti vocali come Siri o Alexa.
- Analisi delle serie temporali : Previsione di andamenti finanziari, meteo o consumi energetici.
Impatto sulle Applicazioni Reali
Queste architetture hanno permesso di superare molte limitazioni delle MLP, rendendo possibile l'elaborazione di dati complessi e ad alta dimensionalità. Tuttavia, richiedono risorse computazionali significative e dataset di grandi dimensioni per funzionare efficacemente. L'integrazione di tecniche come il “transfer learning” ha mitigato questa necessità, consentendo di riutilizzare modelli pre-addestrati su nuovi compiti con minori quantità di dati.
Riferimenti Bibliografici
1. Reti Neurali e Percettrone
- Rosenblatt, F. (1958). The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain. Psychological Review, 65(6), 386–408.
https://doi.org/10.1037/h0042519- Introduzione del percettrone monostrato e sue applicazioni iniziali.
- Minsky, M., & Papert, S. (1969). Perceptrons: An Introduction to Computational Geometry. MIT Press.
- Critica al percettrone monostrato e limiti nella risoluzione di problemi non linearmente separabili.
- Hinton, G. E., & Anderson, J. A. (1989). Parallel Models of Associative Memory. Psychology Press.
- Discussione sulle reti neurali associative e le loro evoluzioni.
2. Backpropagation e Reti Neurali Multilivello
- Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning Representations by Back-Propagating Errors. Nature, 323(6088), 533–536.
https://www.nature.com/articles/323533a0- Articolo fondamentale sull'introduzione della backpropagation.
- LeCun, Y., Bengio, Y., & Hinton, G. (2015). Deep Learning. Nature, 521(7553), 436–444.
https://www.nature.com/articles/nature14539- Panoramica sullo sviluppo delle reti neurali profonde e loro applicazioni moderne.
- Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press.
https://www.deeplearningbook.org- Testo completo e dettagliato sui principi teorici e pratici del deep learning.
3. Funzioni di Attivazione
- Nair, V., & Hinton, G. E. (2010). Rectified Linear Units Improve Restricted Boltzmann Machines. Proceedings of the 27th International Conference on Machine Learning (ICML).
https://dl.acm.org/doi/10.5555/3104322.3104425- Introduzione della funzione ReLU e suoi vantaggi rispetto alle funzioni tradizionali.
- Glorot, X., Bordes, A., & Bengio, Y. (2011). Deep Sparse Rectifier Neural Networks. Proceedings of the 14th International Conference on Artificial Intelligence and Statistics (AISTATS).
http://proceedings.mlr.press/v15/glorot11a.html- Analisi del comportamento delle reti neurali con attivazioni sparse (ReLU).
- Hochreiter, S. (1998). The Vanishing Gradient Problem During Learning Recurrent Neural Nets and Problem Solutions. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 6(02), 107–116.
https://doi.org/10.1142/S0218488598000094- Discussione sul problema del vanishing gradient e possibili soluzioni.
4. Classificazione Multi-Classe e Softmax
- Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.
- Capitolo dedicato alla classificazione multi-classe e all'uso della funzione softmax.
- Murphy, K. P. (2012). Machine Learning: A Probabilistic Perspective. MIT Press.
- Approfondimento sulle tecniche di classificazione probabilistica e cross-entropy.
5. Transfer Learning e Architetture Specializzate
- Pan, S. J., & Yang, Q. (2010). A Survey on Transfer Learning. IEEE Transactions on Knowledge and Data Engineering, 22(10), 1345–1359.
https://doi.org/10.1109/TKDE.2009.191- Revisione completa sul transfer learning e sue applicazioni.
- He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep Residual Learning for Image Recognition. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR).
https://arxiv.org/abs/1512.03385- Introduzione delle architetture ResNet e loro impatto sul deep learning.
- Vaswani, A., Shazeer, N., Parmar, N., et al. (2017). Attention is All You Need. Advances in Neural Information Processing Systems (NeurIPS).
https://arxiv.org/abs/1706.03762- Presentazione del modello Transformer e sue applicazioni in NLP.
6. Tecniche di Regolarizzazione
- Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., & Salakhutdinov, R. (2014). Dropout: A Simple Way to Prevent Neural Networks from Overfitting. Journal of Machine Learning Research, 15(1), 1929–1958.
https://jmlr.org/papers/v15/srivastava14a.html- Introduzione della tecnica Dropout per prevenire l'overfitting.
- Ioffe, S., & Szegedy, C. (2015). Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. Proceedings of the 32nd International Conference on Machine Learning (ICML).
https://arxiv.org/abs/1502.03167- Descrizione della Batch Normalization e suoi benefici nell'addestramento delle reti.
7. Applicazioni Pratiche
- LeCun, Y., Bottou, L., Bengio, Y., & Haffner, P. (1998). Gradient-Based Learning Applied to Document Recognition. Proceedings of the IEEE, 86(11), 2278–2324.
https://ieeexplore.ieee.org/document/726791- Applicazione delle reti neurali al riconoscimento di caratteri (OCR).
- Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012). ImageNet Classification with Deep Convolutional Neural Networks. Advances in Neural Information Processing Systems (NeurIPS).
https://papers.nips.cc/paper/2012/file/c399862d3b9d6b76c8436e924a68c45b-Paper.pdf- Uso delle CNN per il riconoscimento di immagini su larga scala.
8. Letture Aggiuntive
- Schmidhuber, J. (2015). Deep Learning in Neural Networks: An Overview. Neural Networks, 61, 85–117.
https://doi.org/10.1016/j.neunet.2014.09.003- Panoramica storica e tecnica sullo sviluppo delle reti neurali.
- Chollet, F. (2017). Deep Learning with Python. Manning Publications.
- Guida pratica all'implementazione di modelli deep learning con Keras.
- Zhang, C., Bengio, S., Hardt, M., Recht, B., & Vinyals, O. (2021). Understanding Deep Learning Requires Rethinking Generalization. Communications of the ACM, 64(3), 107–115.
https://doi.org/10.1145/3446776- Discussione critica sulle capacità di generalizzazione delle reti neurali.

Il programma allegato
Il programma è strutturato per dimostrare e confrontare due approcci di classificazione: uno basato su percettroni (sia singolo che multi-classe) e uno su una rete neurale multi-strato (MLP). Di seguito viene presentata una panoramica logica e discorsiva delle componenti principali e delle relative funzionalità:
1. Caricamento e Preprocessing del Dataset
La funzione load_custom_mnist_data ha il compito di simulare un dataset MNIST-like a partire da un’unica immagine (formato griglia 560×560 pixel) contenente cifre. Essa:
- Carica l'immagine e la converte in scala di grigi.
- Suddivide l'immagine in sotto-immagini di 28×28 pixel, ciascuna corrispondente a una cifra.
- Binarizza le immagini, trasformandole in bianco e nero.
- Divide il dataset in training set e test set, rendendo i dati pronti per l’addestramento e la valutazione dei modelli.
2. Implementazione del Perceptron e del Multi-Class Perceptron
La classe Perceptron implementa un semplice classificatore binario:
- Inizializza pesi e bias in maniera casuale.
- Utilizza una funzione di attivazione a gradino: restituisce 1 se l’input è maggiore o uguale a zero, altrimenti 0.
- Durante il training, aggiorna i pesi e i bias secondo la regola:
w = w + η · (y – y_pred) · x
dove η (learning rate) controlla la velocità di apprendimento.
Tuttavia, un singolo Perceptron non è in grado di risolvere problemi non linearmente separabili (come l’XOR) e risulta poco efficace per compiti complessi quali l’OCR.
Per questo motivo, la classe MultiClassPerceptron estende il concetto base:
- Crea un perceptrone per ogni classe (in questo caso 10, per le cifre da 0 a 9).
- Addestra ciascun perceptrone con etichette binarie, distinguendo tra “questa cifra” e “altre cifre”.
- Durante la predizione, il modello sceglie la classe associata al perceptrone che fornisce il punteggio più alto.
Questo approccio, pur essendo semplice, ha dei limiti: non cattura pattern complessi e fatica a gestire la variabilità (come rotazioni o distorsioni) presente nelle immagini.
3. Implementazione della Rete Multi-Layer Perceptron (MLP)
La classe MLP implementa una rete neurale a più strati, in grado di modellare relazioni non lineari e riconoscere pattern complessi, risultando quindi più adatta per compiti di OCR. Le caratteristiche principali sono:
- Struttura:
La rete è composta da uno o più strati nascosti (ad esempio, 64 neuroni) e un layer di output. I pesi vengono inizializzati casualmente. - Funzioni di Attivazione:
- Nei layer intermedi viene usata la funzione sigmoid, che trasforma il net input in un valore compreso tra 0 e 1.
- Nel layer finale, se il parametro output_activation è impostato su "softmax", viene applicata la funzione softmax. Questa funzione trasforma i valori in output in probabilità normalizzate, rendendo il modello particolarmente efficace nella classificazione multi-classe.
- Addestramento tramite Backpropagation:
Il processo di training della rete neurale si basa su due funzioni fondamentali:- forward_propagation:
Questa funzione riceve in input i dati (X) e li propaga attraverso ogni layer della rete. In ciascun layer, viene calcolato il "net input" come combinazione lineare degli input (l’output del layer precedente) con i pesi e il bias, seguito dall’applicazione della funzione di attivazione (sigmoid o softmax). Il risultato è una serie di attivazioni, cioè gli output intermedi e finale della rete. - backward_propagation:
Dopo la forward_propagation, la rete confronta l’output ottenuto con il valore atteso (y_true) e calcola l’errore. Partendo dall’ultimo layer, si calcola il delta (l’errore del layer) e, usando la derivata della funzione di attivazione, questo errore viene propagato all’indietro attraverso la rete. In questo modo, si determinano gli aggiornamenti necessari per pesi e bias tramite la discesa del gradiente, riducendo progressivamente l’errore complessivo.
- forward_propagation:
4. Addestramento, Predizione e Visualizzazione
Il programma allena entrambi i modelli con parametri diversi:
- MultiClassPerceptron: addestrato per 20 epoche con un learning rate di 0.01.
- MLP: addestrato per 200 epoche, con 64 neuroni nascosti e un learning rate di 0.001. In questo caso, se configurato, il layer di output utilizza la softmax per ottenere probabilità normalizzate.
La funzione display_predictions visualizza alcune immagini del test set, mostrando le predizioni affiancate alle etichette vere. Questo permette una valutazione qualitativa immediata delle prestazioni di ciascun modello.
La funzione main coordina l’intero processo: carica il dataset, addestra i modelli (prima il MultiClassPerceptron e poi l’MLP) e infine mostra i risultati e l’accuratezza di ciascun approccio.
5. Confronto e Conclusioni
Il programma evidenzia come:
- Il Perceptron (e di conseguenza il MultiClassPerceptron) sia un modello semplice, adatto solo a problemi linearmente separabili, con prestazioni limitate (circa 60-70% di accuratezza).
- L’MLP, grazie alla sua capacità di apprendere relazioni complesse e di gestire dati non lineari, ottiene risultati superiori (stimati tra l’85% e il 95% di accuratezza). Inoltre, l’uso della softmax nell’ultimo layer, abbinato a una loss function compatibile (come la cross-entropy), migliora ulteriormente la capacità di classificazione.
In sintesi, sebbene il perceptron offra un approccio semplice, la rete MLP si rivela superiore per compiti di riconoscimento di cifre (OCR) grazie alla sua capacità di modellare pattern complessi e generalizzare meglio su dati non visti. Per ulteriori miglioramenti, si potrebbero adottare tecniche come l’utilizzo della funzione ReLU, l’aggiunta di ulteriori strati (aumentando la profondità della rete), e l’applicazione di strategie di regolarizzazione come Batch Normalization e Dropout.